학습 데이터를 이용한 기계 학습과 파라미터 조정은 앞서 언급한 내용대로 어떤 데이터 셋을 가지고 학습을 진행했는가에 따라 파라미터의 값이 바뀌게 된다. 수학적으로 접근하면 학습 데이터에 의해 수식이라는 표현 형식으로 나타내어 프로그램을 운영하게 된다.
대용량의 데이터를 데이터 마이닝을 작업하는데있어 파라미터 조정에 의거한 기계 학습을 진행하는 것은 데이터의 전체적인 추이, 경향 등을 추출하기 위함으로써 통계적인 기법에 의거한다.
통계학에서 학습 데이터가 수치로 주어졌을 때 그 수치를 설명할 수 있는 수식을 "회귀 분석"이라 한다. 회귀 분석의 대표적인 방법으로는 "최소제곱법(Least Squares Method)"가 있다.
1차 방정식으로 표현된 최소제곱법 | 2차 방정식으로 표현된 최소제곱법 |
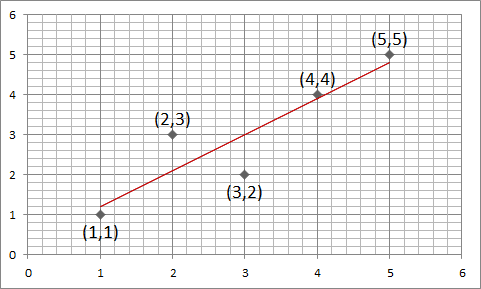
붉은 점은 데이터 포인트라 하며 학습 데이터 셋을 의미한다.
파란 선은 추세선으로 학습 데이터 셋에 의해 만들어진다. 1차 방정식으로 표현된 추세선은 선형 추세선이라 하고, 2차 방정식에 의해 만들어지는 추세선은 곡선 추세선 혹은 다항식 추세선이라 한다. - 추세선의 종류
다음과 같은 5개의 학습 데이터 셋이 있다고 가정하고 선형 추세선을 그리기 위한 1차 방정식을 최소제곱법을 통해 구해보자.
주어진 데이터 포인트는 2개의 미지수(a, b)를 가지는 연립 일차 방정식을 얻는다. 이 연립 방정식은 해를 갖지 않을 수 있다. 이유는 하나의 직선으로 표현 할 수 없기 때문이다. 다시 이 연립방정식들은 다음과 같이 표현할 수 있다.
이렇게 표현한 식에서 행렬 A의 전치를 양 변에 곱한 식을 "정규시스템(Normal System)"이라 하며, 이 정규 시스템을 통해 구해지는 a와 b의 해를 "최소제곱해(Least Square Solution)"라 한다.
이제 위에서 언급한 다섯개의 데이터 포인트를 이용하여 다음과 같이 계산 할 수 있다.
좌변 우변을 각각 연산을 하면 다음과 같이 계산이 된다.
이를 통해 a와 b에 대한 연립 방정식을 구하게 되고,
연립방적식을 통해 a와 b의 해를 구할 수 있다.
이를 식으로 표현하면 다음과 같고,
이 식을 도표에 표시하면 다음과 같이 나온다.
구해진 방정식에 데이터 셋의 x값을 대입해 y값을 구하면 오차는 다음과 같이 나온다.
앞서 계속 언급되는 파라미터 조정과 학습에서 학습 데이터 셋에 따라 파라미터는 크게 바뀐다고 언급하고 있다. 만약 너무 동떨어진 데이터를 사용하게 되면 어떤 결과를 보게 될 것인가?
최소제곱법을 이용하여 구한 선형 추세선은 때로는 위와 같이 오차가 너무 커지는 경우도 발생한다. 이는 학습 시킨 데이터 셋의 문제가 될 수 있으며, 꼭 이 데이터를 학습시켜야 한다면 선형 추세선이 아닌 형태에 맞는 다항식 추세선으로 바꿔 사용해야 한다.
참조
http://matrix.skku.ac.kr/sglee/krf-1/linearalgebra/multimediaproject/14week/21402/page2.htm
http://kingfen.com.ne.kr/left/html/excel/excel2/excel2_19.html
http://ko.wikipedia.org/wiki/%EC%B5%9C%EC%86%8C%EC%A0%9C%EA%B3%B1%EB%B2%95
http://ko.wikipedia.org/wiki/%ED%9A%8C%EA%B7%80%EB%B6%84%EC%84%9D
'Information Technology > Machine Learning' 카테고리의 다른 글
| [기계 학습] N-그램을 이용한 텍스트 마이닝 (0) | 2014.04.10 |
|---|---|
| [기계 학습] 기계 학습의 역사 2 (0) | 2014.04.06 |
| [기계 학습] 기계 학습의 역사 1 (0) | 2014.04.02 |
| [기계 학습] 기계학습이란? (0) | 2014.03.31 |